GAN

基础知识

结构

生成对抗网络（GAN，Generative Adversarial Networks）的基本原理其实非常简单，以生成图片为例，假设我们有两个网络，G（Generator）和D（Discriminator），它们的功能分别是:

  • G是一个生成图片的网络，它接收一个随机的噪声z，通过这个噪声生成图片，记做G(z)。

  • D是一个判别网络，接收一张图片，输出D(x)代表x为真实图片的概率。

在训练过程中，生成网络G的目标就是尽可能生成真实的图片去欺骗判别网络D；而D的目标就是尽量把G生成的图片和真实的图片分别开来。这样，G和D构成了一个动态的“博弈过程”。

在最理想的状态下，最后博弈的结果是：G可以生成足以“以假乱真”的图片G(z)；而D因为难以判定G生成的图片究竟是不是真实的，\(D(G(\boldsymbol{z}))=0.5\) 。这样我们的目的就达成了，用数学语言描述这一过程如下：

\[\min_G \max_D V(D, G) = \mathbb{E}_{\boldsymbol{x}\sim p_{data}(\boldsymbol{x})}[\log D(\boldsymbol{x})] + \mathbb{E}_{\boldsymbol{z}\sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))]\]

其中， \(\boldsymbol{x}\) 表示真实图片， \(\boldsymbol{z}\) 表示输入G网络的噪声， \(G(\boldsymbol{z})\) 表示G网络生成的图片， \(D(\boldsymbol{x})\) 表示D网络判断真实图片是否真实的概率。

  • G的目的： \(D(G(\boldsymbol{z}))\) 是D网络判断G生成的图片是否真实的概率，G应该希望自己生成的图片“越接近真实越好”。也就是说，G希望 \(D(G(\boldsymbol{z}))\) 尽可能得大，这时 \(V(D, G)\) 会变小。因此 \(\min_G\) 。

  • D的目的：D的能力越强，D(x)应该越大， \(D(G(\boldsymbol{z}))\) 该越小, 这时 \(V(D,G)\) 会变大。因此 \(\max_D\)

注解

对于生成器，Goodfellow一开始提出来一个损失函数，后来又提出了一个改进的损失函数，分别是

\(\mathbb{E}_{\boldsymbol{z}\sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))]\) 在最优判别器下等价于最小化生成分布与真实分布之间的JS散度

\(\mathbb{E}_{\boldsymbol{z}\sim p_{\boldsymbol{z}}(\boldsymbol{z})}[- \log D(G(\boldsymbol{z}))]\) 在最优判别器下等价于既要最小化生成分布与真实分布之间的KL散度，又要最大化其JS散度

前者会导致：判别器越好，生成器梯度消失越严重

后者会导致：两个问题，一是梯度不稳定，二是collapse mode即多样性不足

存在的问题

GAN目前存在的主要问题:

  1. 不收敛（non-convergence）的问题: 所有的理论都认为 GAN 应该在纳什均衡（Nash equilibrium）上有卓越的表现，但梯度下降只有在凸函数的情况下才能保证实现纳什均衡。当博弈双方都由神经网络表示时，在没有实际达到均衡的情况下，让它们永远保持对自己策略的调整是可能的

  2. 原始目标函数没有意义，难以训练/崩溃问题（collapse problem）:GAN模型被定义为极小极大问题，没有损失函数，在训练过程中很难区分是否正在取得进展。GAN的学习过程可能发生崩溃问题（collapse problem），生成器开始退化，总是生成同样的样本点，无法继续学习。当生成模型崩溃时，判别模型也会对相似的样本点指向相似的方向，训练无法继续。

  3. 自由度过高：无需预先建模，模型过于自由不可控

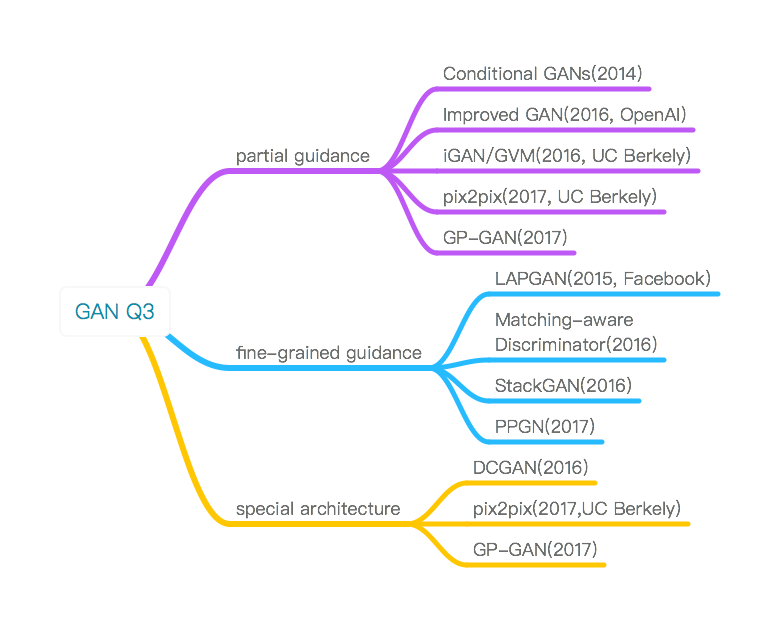
解决问题3的工作：

  • partial guidance: 为原始GAN加上一些显式的外部信息

  • fine-grained guidance: 让GAN的生成过程拆解到多步，从而实现“无监督”

  • special architecture

../_images/GAN_solution3.png

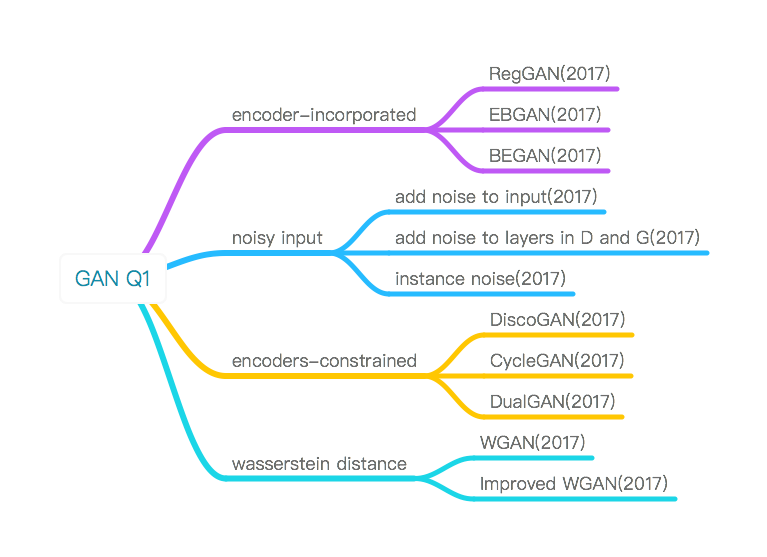
解决问题1的工作：

  • encoder-incorporated: 在原始G和D之上再加上一个自动编码器

  • noisy input:

  • encoders-constrained:

../_images/GAN_solution1.png

一些训练技巧

GAN的变形

CGAN

条件生成式对抗网络（CGAN, Conditional Generative Adversarial Nets）

在生成模型（D）和判别模型（G）的建模中均引入条件变量y（conditional variable y），使用额外信息y对模型增加条件，可以指导数据生成过程。

DCGAN

深度卷积生成式对抗网络(DCGAN，Deep Convolutional Generative Adversarial Nerworks)指出了许多对于GAN这种不稳定学习方式重要的架构设计和针对CNN这种网络的特定经验。

DCGAN的原理和GAN是一样的，只是把G和D换成了两个卷积神经网络。但不是直接换就可以了，DCGAN对卷积神经网络的结构做了一些改变，以提高样本的质量和收敛的速度：

  • 取消所有pooling层。G网络中使用转置卷积（transposed convolutional layer）进行上采样，D网络中用加入stride的卷积代替pooling。

  • 在D和G中均使用batch normalization

  • 去掉FC层，使网络变为全卷积网络

  • G网络中使用ReLU作为激活函数，最后一层使用tanh

  • D网络中使用LeakyReLU作为激活函数

DCGAN-tensorflow(github)

ACGAN（辅助类别的GAN）

GAN不同的是它在判别器D的真实数据x也加入了类别c的信息，这样就进一步告诉G网络该类的样本结构如何，从而生成更好的类别模拟

LSGAN

传统GAN中, D网络和G网络都是用简单的交叉熵loss做更新, 最小二乘GAN则用最小二乘(Least Squares) Loss 做更新:

\[ \begin{align}\begin{aligned}L_D &= \mathbb{E}[(D(\boldsymbol{x})-1)^2] + \mathbb{E}[D(G(\boldsymbol{z}))^2]\\L_G &= \mathbb{E}[D(G(\boldsymbol{z})-1)^2]\end{aligned}\end{align} \]

选择最小二乘Loss做更新有两个好处,

  1. 更严格地惩罚远离数据集的离群Fake sample, 使得生成图片更接近真实数据(同时图像也更清晰)

  2. 最小二乘保证离群sample惩罚更大, 解决了原本GAN训练不充分(不稳定)的问题:

但缺点也是明显的, LSGAN对离群点的过度惩罚, 可能导致样本生成的”多样性”降低, 生成样本很可能只是对真实样本的简单”模仿”和细微改动

LAPGAN

拉普拉斯金字塔生成式对抗网络(LAPGAN, Laplacian Pyramid of Adversarial Networks)

不要让 GAN 一次完成全部任务，而是一次生成一部分，分多次生成一张完整的图片

eyescream(github)

pix2pix

pix2pix 中 G 和 D 使用的网络都是 U-Net 结构，是一种 encoder-decoder 完全对称的结构，并且在这样的结构中加入了 skip-connection 的使用, 效果十分惊艳

kip-connection 不仅使得梯度传导更通畅，网络训练更容易，也因为这类工作多数是要学习图片之间的映射，那么让 encoder 和 decoder 之间一一对应的层学到尽可能匹配的特征将会对生成图片的效果产生非常正面的影响。

WGAN

令人拍案叫绝的Wasserstein GAN

  • 彻底解决GAN训练不稳定的问题，不再需要小心平衡生成器和判别器的训练程度

  • 基本解决了collapse mode的问题，确保了生成样本的多样性

  • 训练过程中终于有一个像交叉熵、准确率这样的数值来指示训练的进程，这个数值越小代表GAN训练得越好，代表生成器产生的图像质量越高

  • 以上一切好处不需要精心设计的网络架构，最简单的多层全连接网络就可以做到

而改进后相比原始GAN的算法实现流程却只改了四点：

  • 判别器最后一层去掉sigmoid

  • 生成器和判别器的loss不取log

  • 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c

  • 不要用基于动量的优化算法（包括momentum和Adam），推荐RMSProp，SGD也行

但是, 有时一味地通过裁剪weight参数的方式保证训练稳定性, 可能导致生成低质量低清晰度的图片, 因此出现了 WGAN-GP

互怼的艺术：从零直达 WGAN-GP

WGAN-GP舍弃裁剪D网络weights参数的方式, 而是采用裁剪D网络梯度的方式(依据输入数据裁剪), WGAN-GP在某些情况下是WGAN的改进, 但是如果你已经用了一些可靠的GAN方法, 其实差距并不大.

BGAN（Boundary-Seeking GAN）

BGAN优势在于生成离散样本（当然像图像这样的连续样本也可以支持）。

BGAN的生成器以不断生成决策边界上的样本为目标

EBGAN

EBGAN在边缘的生成效果上更流畅, 而且加了特殊的正则项, 在生成的类别上, EBGAN更倾向于生成不同的脸型和人种

SGAN(Stacked GAN)

SGAN是一种结构创新的GAN，通过堆叠多个GAN网络，实现生成模型的信息“分层化”

GAN 在NLG/NTG中的应用

GAN为何不能直接用于文本生成 1

啥是离散型数据？

这里所谓的离散，并不是指：文本由一个词一个词组成，而是指文本本身的取值是不连续的

GAN的作者早在原版论文时就提及，GAN只适用于连续型数据的生成，对于离散型数据效果不佳，原因在于，当前神经网络的优化方法大多数都是基于梯度的，GAN在面对离散型数据时，判别网络无法将梯度Back propagation（BP）给生成网络。

我们知道，基于梯度的优化方法大致意思是这样的，微调网络中的参数，看看最终输出的结果有没有变得好一点，有没有达到最好的情形。

但是对于离散数据，判别器D从生成器G得到的是Sampling (即将softmax输出的结果过渡到One-hot vector 然后再从词库中查询出对应index的词)之后的结果，也就是说，经过参数微调之后，即便softmax的输出优化了一点点，但是G输出的结果还是跟以前一模一样，并再次将相同的答案重复输入给D，这样D给出的评价就会毫无意义，G的训练也会失去方向。

那么能不能每次给D直接吃Sampling之前的结果，也就是softamx输出的那个distribution? 答案是否定的。判别器D的初衷是为了准确辨别生成样本和真实样本的，当生成样本是一个充满了float小数的分布，而真实样本是一个One-hot Vector时，判别器D很容易“作弊”，它根本不用去判断生成分布是否与真实分布更加接近，它只需要识别出给到的分布是不是除了一项是 1，其余都是0就可以了。所以无论Sampling之前的分布多么接近于真实的One-hot Vector，只要它依然是一个概率分布，都可以被判别器D轻易地检测出来。

上面所说的原因当然也有数学上的解释，生成样本的loss衡量标准是JS散度，它在应用上其实是有弱点的，它只能被正常地应用于互有重叠（Overlap）的两个分布，当面对互不重叠的两个分布 \(P\) 和 \(Q\) ，其JS散度：

\[JSD(P\parallel Q) \equiv log2\]

因此，除非softmax能output出与真实样本 exactly 相同的独热分布（One-hot Vector）（当然这是不可能的），否则，生成器无论怎么做基于Gradient 的优化，输出分布与真实分布的始终是 \(log2\) ，G的训练于是失去了意义。

1

https://zhuanlan.zhihu.com/p/29168803