概率论

stanford cs229 prob

概念汇总

概率函数 累积分布函数/概率分布函数/分布函数(cumulative distribution function, CDF): \(F_X(x) = Pr(X\le x)\) 概率密度函数（probability density function (PDF)）: PDF 就是 CDF 的导数 \(Pr(a\e X\le b)= \int_a^bf_X(x)dx\) 概率质量函数（probability mass function, PMF）: 针对离散变量，实际与PDF等价

先验概率(prior) \(p(\theta)\) :因的概率分布 后验概率(posterior) \(p(\theta|x)\) :知道果后，估计因的概率分布 似然函数(likelihood) \(p(x|\theta)\) :先确定原因，根据原因来估计结果的概率分布 (evidence) \(p(x)\) : 只看结果的概率分布

贝叶斯公式
\[p(\theta|x) = \frac{p(x|\theta)p(\theta)}{p(x)}\]

协方差与相关系数

协方差(covariance)

(1)\[Cov[X, Y] = E[(X-E(X))(Y-E(Y))] = \frac{\vec{x} \cdot \vec{y}}{n}\]

通俗理解为两个变量在变化过程中是同方向变化？还是反方向变化？同向或反向程度如何？

从数值来看，协方差的数值越大，两个变量同向程度也就越大。反之亦然。

协方差为0，则两个变量不相关（uncorrelated）/不线性相关

由于协方差会受变量变化幅度(向量长度)的影响，为了消除这种影响，准确地研究两个变量在变化过程中的相似程度，引入了相关系数

相关系数

(2)\[\begin{split}\rho &= \frac{Cov[X, Y]}{\sigma _X \sigma _Y} \\ &= \frac{\vec{x} \cdot \vec{y}}{\lVert \vec{x} \rVert \lVert \vec{y} \rVert} = \cos(\theta) \\ \sigma _X &= \sqrt{E((X-\mu _X)^2)}\end{split}\]

相关系数可以看成剔除了两个变量量纲影响、标准化后的特殊协方差。

从向量角度看，相关系数其实就是余弦距离。

  • \(0 < \rho \leq 1\) ，则正相关

  • \(-1 \leq \rho < 0\) ，则负相关

  • \(\rho=0\) ，则不相关, 不相关只是说二者没有 线性 关系，但并不代表没有任何关系。

注解

要说明的一点是， \(\rho=0\) 代表不相关(uncorrelated)，并不一定独立(independent)。 独立是不相关的充分不必要条件，即独立可以推出不相关，反之不行(高斯过程里二者等价)。

例如 \(Y=X^2\), X和Y不相关，但是它们并不独立

协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差，因此就有了协方差矩阵

协方差矩阵

\[\Sigma _{ij} = Cov[X_i, Y_j]\]

协方差矩阵是一个对称的矩阵，而且对角线是各个维度的方差。

独立(independence)

\[P(X, Y) = P(X)P(Y)\]

则 X、Y 相互独立

不相关与独立

不相关未必独立，但独立一定不相关。

不相关只说明不存在线性相关，但未必不存在其它相关;而独立表示完全无关

常见分布

均匀分布(distribution)

\[U[0, 1]\]

伯努利分布(Bernoulli distribution)

如：抛硬币正面朝上的概率

\[\begin{split}f(x)=p^x(1-p)^{1-x}=\left \{ \begin{array}{ll} p & \textrm{if $x =1$} \\ 1-p&\textrm{if $x=0$} \\ 0 & \textrm{otherwise} \end{array} \right.\end{split}\]

二项分布(Binomial distribution)

如：扔n次硬币

\[ \begin{align}\begin{aligned}X &\sim B(n, p)\\f(x) &= (_{n}^{x} )p^{x} (1-p)^{n-x}\end{aligned}\end{align} \]

多项分布(Multinomial Distribution)

如：扔骰子

贝塔分布(Beta distribution)

狄利克雷分布(Dirichlet distribution)

泊松分布

正态分布（Normal distribution）

又名高斯分布（Gaussiandistribution）

标准正态分布： \(\mathcal{N}(0, 1)\)

多变量正态分布

多变量正态分布是正态分布在多维变量下的扩展，也称为多变量高斯分布。它的参数是一个均值向量(mean vector) \(\mu\) 和协方差矩阵 (covariance matrix) \(\Sigma \in R^{n\times n}\) ，其中 n 是多维变量的向量长度， \(\Sigma \ge 0\) 是对称正定矩阵。多变量正态分布的概率密度函数为：

\[p(x;\mu,\Sigma)=\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)\]

其中， \(|\Sigma|\) 是矩阵 \(\Sigma\) 的行列式。对于服从多变量正态分布的随机变量 \(x\) ，其均值由下面的公式得到：

\[E[x]=\int_xxp(x;\mu,\Sigma)dx=\mu\]

对随机向量参数 \(Z\) ，其协方差计算公式为：

\[\mathrm{Cov}(Z)=E[(Z-E[Z])(Z-E[Z])^T]=E[ZZ^T]-(E[Z])(E(Z))^T\]

因此，对于 \(X\sim N(\mu,\Sigma)\)

\[\mathrm{Cov}(X)=\Sigma\]

接下来，看几组二元正态分布的概率密度的图形：

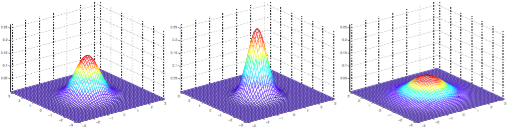
../_images/prob_gauss_1.png

\(\mu=0\) ( \(2\times 1\) 的零向量)时，随 \(\Sigma\) ( \(2\times 2\) 的矩阵)的变化。(a) \(\Sigma=I\)；(b) \(\Sigma=0.6I\) ；(c) \(\Sigma=2I\)

交叉熵（cross entropy）和相对熵（relative entropy）

../_images/KL-CE-MLE.jpg
交叉熵
(3)\[CE(p \parallel q) = -\int p(x) \ln q(x) dx\]
相对熵

就是KL散度（Kullback–Leibler divergence），用于衡量两个概率分布之间的差异。

(4)\[\begin{split}KL(p \parallel q) &= -\int p(x) \ln q(x) dx - (-\int p(x) \ln p(x) dx) \\ & = -\int p(x) \ln \left[\frac{q(x)}{p(x)}\right]dx\end{split}\]

重要

KL 散度不满足对称性，即 \(KL(p \parallel q) \neq KL(q \parallel p)\), 因为KL散度不满足对称性和勾股定理，因此其不能作为“距离”理解

理解:

1）信息熵：编码方案完美时，最短平均编码长度的是多少。
2）交叉熵：编码方案不一定完美时（由于对概率分布的估计不一定正确），平均编码长度的是多少。
平均编码长度 = 最短平均编码长度 + 一个增量
3）相对熵：编码方案不一定完美时，平均编码长度相对于最小值的增加值。（即上面那个增量

TODO

difference between ica , pca and lda

pca 是降维，ica 是信号的源分解