性能指标

分类问题

Recall & Precision

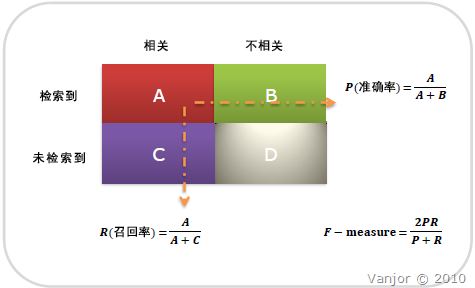
../_images/recall.png
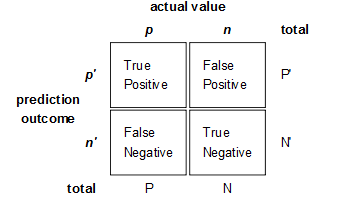
../_images/recall2.png

混淆矩阵(confusion matrix)

  • 召回率/真阳性/查全率(Recall) = 系统检索到相关文件/系统所有相关的文件总数

\[R = \frac{TP}{TP+FN}\]

  • 准确率/查准率(Precision) = 系统检索到的相关文件/系统所有检索到的文件总数

\[P = \frac{TP}{TP+FP}\]

注解

准确率和召回率是互相影响的，理想情况下肯定是做到两者都高，但是一般情况下准确率高、召回率就低，召回率低、准确率高，当然如果两者都低，那是什么地方出问题了。一般情况，用不同的阀值，统计出一组不同阀值下的精确率和召回率

如果是做搜索，那就是保证召回的情况下提升准确率；如果做疾病监测、反垃圾，则是保准确率的条件下，提升召回。

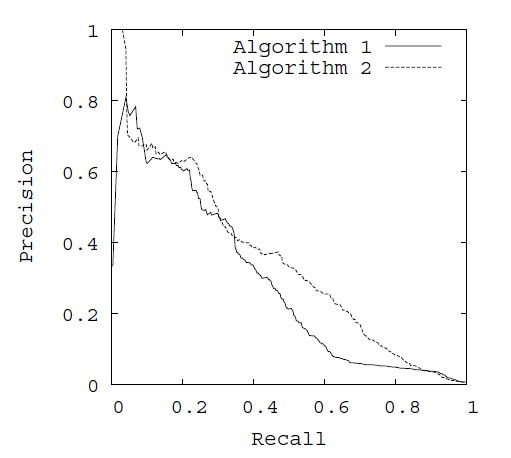
../_images/PR_curve.jpg

PR curve

为了平衡精确率和召回率的影响，较为全面地评价一个分类器，引入F-score 来衡量。

  • F-score: 权衡精度和召回率(精度和召回率的调和平均)

    \[F_{\beta} = \frac{(1+\beta^2)\times P\times R}{\beta^2 \times P + R}\]

    其中，\(\beta （ \beta > 0 ）\) 的取值反映了精确率和召回率在性能评估中的相对重要性具体，通常情况下，取值为1。

    • 当 \(\beta = 1\) 时，就是常用的 \(F_1\) 值(平衡 F 分数)，表明精确率和召回率一样重要

      \[\begin{split}\frac{2}{F_1} &= \frac{1}{P} + \frac{1}{R} \\ F_1 &= \frac{2PR}{P+R}\end{split}\]

    • 当 \(\beta = 2\) 时， 表明召回率的权重比精确率高；

    • 当 \(\beta = 0.5\) 时， 表明精确率的权重比召回率高。

  • G-mean: 评价不平衡数据的模型表现

    \[G-mean = \sqrt{\frac{TP}{TP+FN}\times\frac{TN}{TN+FP}}\]

  • accuracy

    \[acc = \frac{TP+TN}{TP+TN+FP+FN}\]

Macro-averaging & Micro-averaging

F-score 评估指标适用于二分类问题，但当我们的问题属于多分类问题时，在不同类别下综合考察分类器的优劣就要用到宏平均和微平均。

  • 宏平均(Macro-averaging): 先对每一个类统计指标值，然后再对所有类求算术平均值。

    一种说法：

    \[F_{macro} = \frac{1}{n} \sum_{i=1}^n F_i\]

    另一种说法：

    \[\begin{split}P_{macro} &= \frac{1}{n} \sum_{i=1}^n P_i \\ R_{macro} &= \frac{1}{n} \sum_{i=1}^n R_i \\ F_{macro} &= \frac{2\times P_{macro} \times R_{macro}}{P_{macro} + R_{macro}}\end{split}\]

  • 微平均(Micro-averaging): 先对数据集中的每一个示例不分类别进行统计，建立全局混淆矩阵，然后计算相应的指标。

    \[\begin{split}P_{micro} &= \frac{\bar{TP}}{\bar{TP} + \bar{FP}} = \frac{\sum_{i=1}^n {TP}_i}{\sum_{i=1}^n {TP}_i + \sum_{i=1}^n {FP}_i} \\ R_{micro} &= \frac{\bar{TP}}{\bar{TP} + \bar{FN}} = \frac{\sum_{i=1}^n {TP}_i}{\sum_{i=1}^n {TP}_i + \sum_{i=1}^n {FN}_i} \\ F_{micro} &= \frac{2 \times P_{micro} \times R_{micro}}{P_{micro} + R_{micro}}\end{split}\]

宏平均与微平均的不同之处在于：宏平均赋予 每个类 相同的权重，然而微平均赋予 每个样本决策 相同的权重。因为从 \(F_1\) 值的计算公式可以看出，它忽略了被分类器正确判定为负类的样本，其大小主要由被分类器正确判定为正类的那些样本决定，在微平均评估指标中，样本数多的类别主导着样本数少的类。因而在测试数据集上，度量分类器对大类判别的有效性应该选择微平均，而度量分类器对小类判别的有效性则应该选择宏平均。

mAP

平均精度均值(mean average precision, mAP) 可以由它的三个部分来理解：P, AP, mAP。

P (Precision)即前述准确率，它只考虑了返回结果中相关文档的个数，没有考虑文档之间的序。对一个搜索引擎或推荐系统而言返回的结果必然是有序的，而且越相关的文档排的越靠前越好，于是有了 AP 的概念。

对一个有序的列表，计算 AP (average Precision) 的时候要先求出每个位置上的 Precision，然后对所有的位置的 Precision 再做 average。所以 AP 也就是 PR曲线 下的面积，这里 average 是对 recall 取平均。

而 mAP (mean average precision) 的 mean，是对所有类别取平均。

以分类问题为例，mAP的过程如下：

  1. 先把所有bbox找出来 并加上confidence

  2. 然后每类根据confidence从大到小排列

  3. 每个confidence算出其recall和precision得到每一类的ap曲线

  4. 取mean

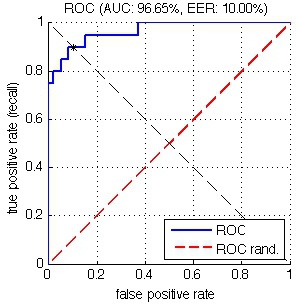
ROC & AUC

ROC(Receiver Operating Characteristic) 和 AUC(Area Under roc Curve)是评价分类器的指标，上面第一个图的ABCD仍然使用，只是需要稍微变换。

ROC关注两个指标

  • True Positive Rate ( TPR/Recall )  = TP / [ TP + FN] ，TPR代表能将正例分对的概率

  • False Positive Rate( FPR ) = FP / [ FP + TN] ，FPR代表将负例错分为正例的概率

在 ROC 空间中，每个点的 横坐标是FPR，纵坐标是TPR ，这也就描绘了分类器在 TP（真正的正例）和 FP（错误的正例）间的trade-off。ROC 的主要分析工具是一个画在 ROC 空间的曲线—— ROC curve。我们知道，对于二值分类问题，实例的值往往是连续值，我们通过设定一个阈值，将实例分类到正类或者负类（比如大于阈值划分为正类）。因此我们可以变化阈值，根据不同的阈值进行分类，根据分类结果计算得到 ROC 空间中相应的点，连接这些点就形成 ROC curve。ROC curve经过 (0, 0) (1, 1)，实际上 (0, 0) 和 (1, 1) 连线形成的 ROC curve 实际上代表的是一个随机分类器。一般情况下，这个曲线都应该处于 (0, 0) 和 (1, 1) 连线的上方。如图所示:

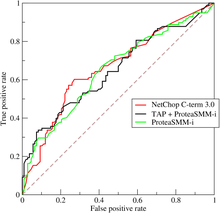
../_images/roc.png

ROC curve

用 ROC curve 来表示分类器的 performance 很直观好用。可是，人们总是希望能有一个数值来标志分类器的好坏。于是 AUC 就出现了。顾名思义，AUC 的值就是处于 ROC curve 下方的那部分面积的大小。通常，AUC 的值介于0.5到1.0之间，较大的 AUC 代表了较好的 Performance。

注解

AUC 用得比较多的原因是， 实际环境中正负样本极不均衡，PR 曲线会受此影响出现较大浮动，无法很好反应出分类器性能；而ROC受此影响较小。

AUC计算工具

参考链接： http://www.vanjor.org/blog/2010/11/recall-precision/ http://bubblexc.com/y2011/148/ http://wenku.baidu.com/view/ef91f011cc7931b765ce15ec.html

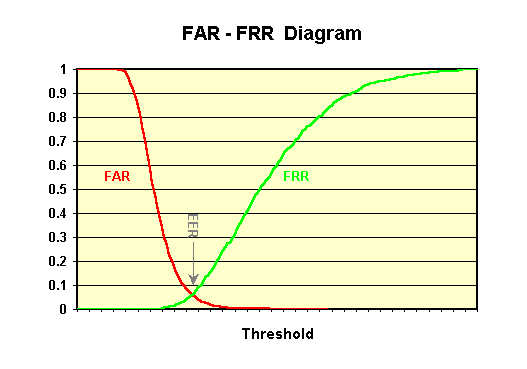
FRR, FAR & EER

参考链接

  • 错误拒接率(False Rejection Rate, FRR) 的标准称谓是FNMR(False Non-Match Rate 不匹配率)，表示本该正确的样本未被识别出来的概率 = Miss/Total_True

  • 错误接受率(False Acceptance Rate, FAR)，表示本该错误的样本被错误地识别为正确的概率 = False Alarm/ Total_False

  • 相等错误率(Equal Error Rate, EER), 主要用于评价分类算法的整体性能。它将 FAR、FRR 两个参数统一为一个参数。FAR 随阈值增大而减小，FRR随阈值增大而增大，当到某一点，两条曲线相交(FRR=FAR)，这时的阈值就是等错误率阈值，有EER=FR=FA。EER 表示的是准确率和召回率的折衷，因此其也可以定义为：the Equal Error Rate (EER) is the point on the ROC curve that corresponds to have an equal probability of miss-classifying a positive or negative sample. This point is obtained by intersecting the ROC curve with a diagonal of the unit square。下面列出了两种定义下该点的位置，显然，EER 值越小的时候，分类器的整体性能越高。

    ../_images/EER_1.gif ../_images/EER_2.jpg

聚类问题

Jaccard 距离

兰德系数

互信息

轮廓系数

NLG

../_images/NLG_metric.png

metrics for nlg

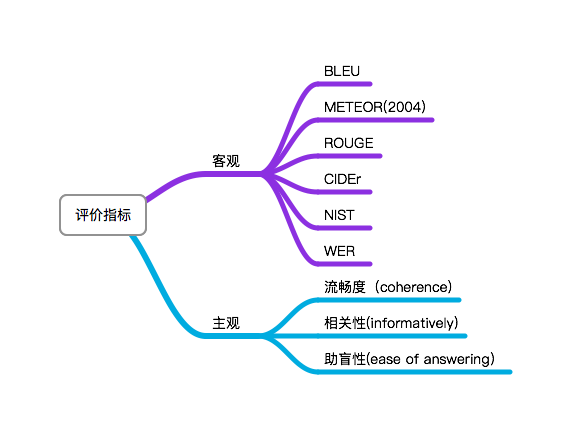
BLEU

双语互译质量评估辅助工具(BiLingual Evaluation Understudy, BLEU) 通过将一句机器翻译的话与其相对应的几个参考翻译作比较，算出一个综合分数，判断两个句子的相似程度。

BLEU实质是对两个句子的 共现词频率 计算。

(1)\[BLEU = BP \times \exp{(\sum_{n=1}^N w_i \log P_n)}\]
(2)\[\begin{split}P_n &= \frac{\displaystyle{\sum_{c\in{\mathrm{candidates}}}} \displaystyle{\sum_{n-gram\in c}} \mathrm{Count}_{clip} (\mathrm{n-gram})}{\displaystyle{\sum_{c'\in{\mathrm{candidates}}} \displaystyle{\sum_{n-gram' \in c'}} \mathrm{Count} (\mathrm{n-gram}')}} \\ \mathrm{Count}_{clip} &= \min\{\mathrm{Count}_{w_i}, \mathrm{Ref\_Count}_{w_i}\} \\ \mathrm{Ref\_Count}_{w_i} &= \max\{\mathrm{Ref}_j\_\mathrm{Count}_{w_i}\} j = 1,2,...\end{split}\]
(3)\[\begin{split}BP = \left\{ \begin{array}{ll} 1 & \textrm{if } l_c > l_s \\ e^{1-\frac{l_s}{l_c}} & \textrm{if } l_c \le l_s \end{array} \right.\end{split}\]

其中 \(P_n\) 是N-gram 精度, 一般情况1-gram反映的是这篇译文的充分性, 2-gram以上反映的是译文的流畅性; \(P_n\) 的分母表示candidate 中的 n-gram 个数，分子表示参考译文和candidate的截断n-gram； \(BP\) 是惩罚因子, \(l_c\) 代表表示机器翻译译文的长度， \(l_s\) 表示参考答案的有效长度

  • \(\mathrm{Ref}_j\_\mathrm{Count}_{w_i}\) : 词 \(w_i\) 在第 \(j\) 个参考译文里出现的次数

  • \(\mathrm{Count}_{w_i}\) : candidate 中词 \(w_i\) 的个数

缺点:

  1. 不考虑语言表达（语法）上的准确性；

  2. 测评精度会受 常用词 和 短译句 的干扰；

  3. 没有考虑同义词或相似表达的情况，可能会导致合理翻译被否定；

NIST

weighted version of BLEU, with more importance given to less frequent n-grams

ROUGE

ROUGE(Recall-Oriented Understudy for Gisting Evaluation) 是从召回率的角度计算，常用于自动摘要任务和机器翻译的评价

N-gram co-ccurence metrics measuring content overlaps

\[\mathrm{ROUGH}_n = \frac{\displaystyle{\sum_{C\in{\{Model Units\}}}} \displaystyle{\sum_{n-gram\in{C}}} Count_{match} (n-gram)}{\displaystyle{\sum_{C\in{\{Model Units\}}}} \displaystyle{\sum_{n-gram\in{C}}} Count (n-gram)}\]

METEOR

METEOR(Metric for Evaluation of Translation with Explicit ORdering) 的目的是解决BLEU中的固有缺陷，METEOR 还有一些其他指标不具备的功能，如同义词匹配

召回率基础上的指标相比于单纯基于精度的指标(如BLEU、NIST), 其结果和人工判断的结果有较高相关性

计算METEOR 首先要对两个句子中的unigram 进行对齐，得到一组 alignment (a set of mappings between unigrams), 对齐原则如下：

  • every unigram in the candidate translation must map to zero or one unigram in the reference

  • If there are two alignments with the same number of mappings, the alignment is chosen with the fewest crosses

据此计算unigram precision \(P\) 和 Unigram recall \(R\)

\[\begin{split}P = \frac{m}{\omega _t} \\ R = \frac{m}{\omega _r}\end{split}\]

其中，

  • \(m\) 表示 candidate translation 与 reference translation 匹配上的unigram 个数，

  • \(\omega _t\) 表示 candidate translation 中unigram 的个数

  • \(\omega _r\) 表示 reference translation 中unigram 的个数

则unigram precision \(P\) 和 Unigram recall \(R\) 的调和平均

\[\begin{split}F_{\mathrm{mean}} = \frac{(1 + \beta ^2)PR}{\beta ^2 P+ R} \\\end{split}\]

\(\beta\) 一般取为3。以上只考虑了单个词的一致性，没有考虑大的连续块，因此这里引入惩罚因子。首先unigrams are grouped into the fewest possible chunks，penalty \(p\) 定义为

\[p = \gamma (\frac{c}{u_m})^\theta\]

\(\gamma\) 一般取为 0.5，\(\theta\) 一般取为3， 其中，

  • \(c\) 表示 number of chunks

  • \(u_m\) 表示 number of unigrams that have been mapped.

最终， METEOR的定义如下

\[M = F_{\mathrm{mean}}(1-p)\]

NLL

(Negative log-likelihood, NNL)